密码学入门——消息认证码
加密&完整性
Goal
在无需保密性的情况下提供完整性,基本机制如MAC(消息认证码)
MACs
基本组成(发送方和接收方共享同一密钥k)
$$
S(k,m)\to tag\space \space ;V(k,m,tag)\to ‘yes’/‘no’
$$
$$
[其一致性要求为\forall k \in \mathcal{K},m\in \mathcal{M}:V(k,m,S(k,m))=’yes’]
$$
若双方不共享同一密钥k,则难以达到完整性目的保障,比如CRC(循环冗余检验):
$$
CRC(m)\to tag\space ,Verify(m,tag)\stackrel{?}{=} yes
$$
但是攻击者可以直接拦截并伪造新的消息和验证码,从而破解消息。
系统安全性(目标)
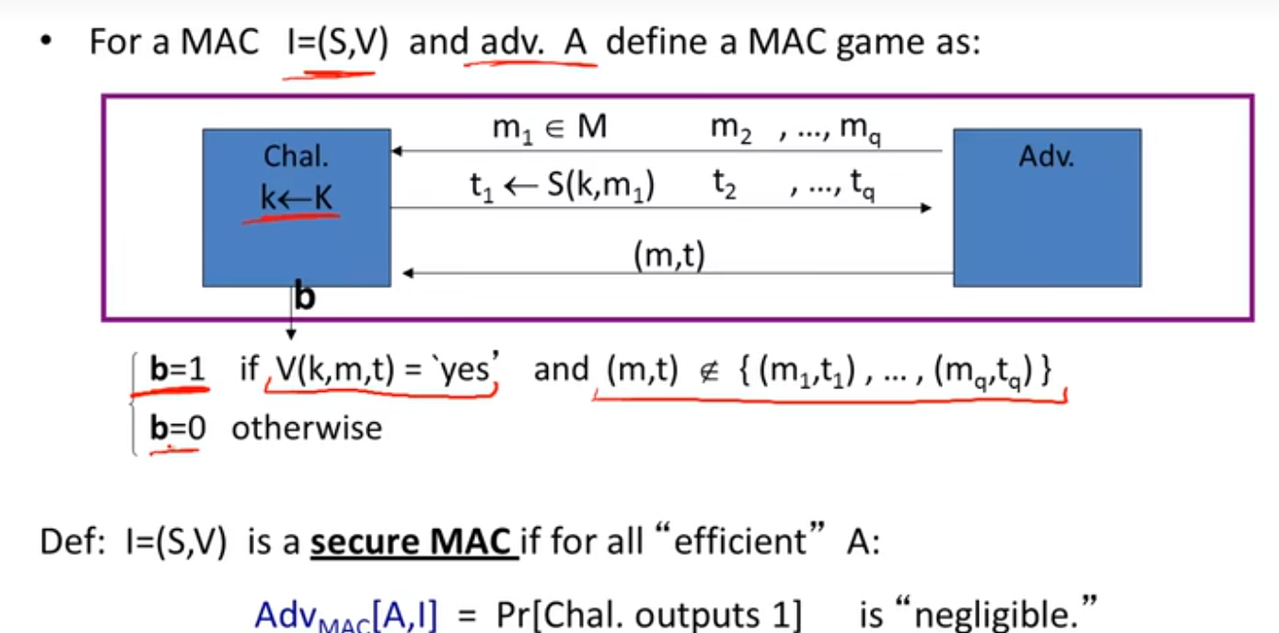
攻击者可以通过m向挑战者寻问其生成的tag,之后攻击者伪造一个新的(m,tag)(优势为挑战者最终输出’yes’的概率大于1/2)若攻击者在已知消息-标签对后,无法为同一消息生成一个新的有效的标签,则此系统处于安全状态(SU-CMA:存在性不可伪造性);
因此为了避免不安全因素(如只有5位mac码情况下,攻击者利用穷举攻击爆破),在构造MAC系统时标签数一般设置为64,96(TLS),128等,以避免过短的标签会因为暴力破解而被爆破。
缺点
仅验证文件内容完整性的认证机制(如MAC),虽然能有效防止数据被直接篡改,却无法防御一种更隐蔽的攻击:攻击者可以在不破坏任何认证标签的前提下,将系统中多个经过认证的合法数据进行交换。例如,病毒将两个未被篡改且MAC校验通过的文件互相调换位置,导致系统在加载错误内容时仍无法察觉,从而破坏其正常逻辑。常见的加固方法(如将文件名纳入认证范围)能缓解此问题,但若攻击发生在更高的逻辑层面(如交换经过认证的数据库记录或通信指令),此类基于单个实体的认证机制依然会失效。
基于PRF(伪随机函数)的MAC构造
$$
设定一个PRF(F:k*m \to t)和一个MAC(I_{F}=(S,V)):\
其中S(k,m):=F(k,m),\space V(k,m,t)\to yes(t=F(k,m))/no
$$
然而,若对于无论何值都只输出10bit的Tag的随机函数并不安全,因为其仍可有1/1024的概率(不可忽略)来穷举爆破,因此对于其安全性的定义如下:
$$
(EU-CMA)假设对于一个随机函数f:X\to Y,攻击者向挑战者发送m_1,m_2,…,m_q(m\in X),\挑战者向攻击者发送回各自对应的tag,如t_1,t_2,…(t\in Y),之后攻击者发送回一个(m,t*)对,\若t\in Y,且m\notin X,则攻击者获胜,此时的获胜概率最多只有\Pr[A_{win}]=\frac{1}{|Y|}\因此我们可以推断出基于PRF的MAC构造中敌手A的优势为Adv_{MAC}[A,I_F]\le Adv_{PRF}[B,F]+\frac{1}{|Y|}\当tag空间足够大时,其(对应的\frac{1}{|Y|})优势可被忽略。
$$
在一些实际应用中,我们发现AES就是一种16字节输入的MAC(以小消息PRF作为输入),若要构造消息空间大规模GB级别的,有HMAC(如SSL,SSH)和CBC-MAC(常用于银行业,如自动清算系统ACH,用于保证在银行间传输支票等信息的完整性)接受小输入PRF生成大输入PRF。(在实际应用中,我们可以在生成后通过截断,在保证可验证性的基础上减少tag的大小)
CBC-MAC
ECBC
$$
设置一个PRP函数(F:KX\to X),定义新的PRF为(F_{ECBC}:K^2X^{\le L}\to X)
$$